Seyedali Mirjalili

Like Moths to A Flame

Have you ever seen a moth flying around your house? If yes, I am sure you wonder why? You may think they love your house or they try to find foods. However, the fact is that the poor little ones get distracted by artificial lights and lose their natural flying path. They all ended up in deadly spiral flying paths. Anyway, I saw many of them in my life and once decided to study about them. At the beginning, I did not mean to inspire from them to propose an optimization algorithm, but as always it eventually inspired me to simulate this behaviour in computer and propose an optimization algorithm :)

All the algorithms that I have proposed so far simulate the behaviour of natural creatures for survival. This algorithm, however, simulates the death behaviour of moths. :D I hope that you do not think I enjoy watching them dying and start blaming me :). Honestly, I always catch them and free them in fresh air when I find them in my house. Anyway, let’s talk about the optimization algorithm that I proposed recently. I am sure you could guess what the name is: Moth Optimizer?!! No, the name is Moth-flame Optimization Algorithm. In my culture and some the culture (I believe), a moth is the symbol of pure love because it gets attracted by a flame and moves towards it until death. That is actually not true as per the reason that I explained above, but this is how a lot of poets described it. Therefore, I have decided to not to ignore the role of flame in this relationship :D and named this algorithm Moth-Flame Optimization Algorithm.

Moths are fancy insects, which are highly similar to the family of butterflies. Basically, there are over 160,000 various species of this insect in nature. They have two main milestones in their lifetime: larvae and adult. The larvae is converted to moth by cocoons. The most interesting fact about moths is their special navigation methods in night. They have been evolved to fly in night using the moon light. They utilized a mechanism called transverse orientation for navigation. In this method, a moth flies by maintaining a fixed angle with respect to the moon, a very effective mechanism for travelling long distances in a straight path [1, 2]. Since the moon is far away from the moth, this mechanism guarantees flying in straight line. The same navigation method can be done by humans. Suppose that the moon is in the south side of the sky and a human wants to go the east. If he keeps moon of his left side when walking, he would be able to move toward the east on a straight line.

Despite the effectiveness of transverse orientation, we usually observe that moths fly spirally around the lights. In fact, moths are tricked by artificial lights and show such behaviours. This is due to the inefficiency of the transverse orientation, in which it is only helpful for moving in straight line when the light source is very far. When moths see a human-made artificial light, they try to maintain a similar angle with the light to fly in straight line. Since such a light is extremely close compared to the moon, however, maintaining a similar angle to the light source causes a useless or deadly spiral fly path for moths [2]. A conceptual model of this behaviour is illustrated as follows:

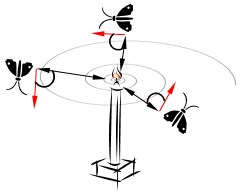The moth eventually converges towards the light. I mathematically modeled this behaviour and proposed an optimizer called Moth-Flame Optimization (MFO) algorithm.

The MFO algorithm

In the proposed MFO algorithm, I assumed that the candidate solutions are moths and the problem’s variables are the position of moths in the space. Therefore, the moths can fly in 1-D, 2-D, 3-D, or hyper dimensional space with changing their position vectors. Since the MFO algorithm is a population-based algorithm.

It should be noted here that moths and flames are both solutions. The difference between them is the way we treat and update them in each iteration. The moths are actual search agents that move around the search space, whereas flames are the best position of moths that obtains so far. In other words, flames can be considered as flags or pins that are dropped by moths when searching the search space. Therefore, each moth searches around a flag (flame) and updates it in case of finding a better solution. With this mechanism, a moth never lose its best solution.

I chose a logarithmic spiral as the main update mechanism of moths in this paper. However, any types of spiral can be utilized here subject to the following conditions:

Spiral’s initial point should start from the moth
Spiral’s final point should be the position of the flame
Fluctuation of the range of spiral should not exceed from the search space

Considering these points, I defined a logarithmic spiral for the MFO algorithm as follows:

where Di indicates the distance of the i-th moth for the j-th flame, b is a constant for defining the shape of the logarithmic spiral, and t is a random number in [-1,1].

D is calculated as follows:

where Mi indicate the i-th moth, Fj indicates the j-th flame, and Di indicates the distance of the i-th moth for the j-th flame.

With the above equations, the spiral flying path of moths is simulated. As may be seen in this equation, the next position of a moth is defined with respect to a flame. The t parameter in the spiral equation defines how much the next position of the moth should be close to the flame (t = -1 is the closest position to the flame, while t = 1 shows the farthest). Therefore, a hyper ellipse can be assumed around the flame in all directions and the next position of the moth would be within this space. Spiral movement is the main component of the proposed method because it dictates how the moths update their positions around flames. The spiral equation allows a moth to fly “around” a flame and not necessarily in the space between them. Therefore, the exploration and exploitation of the search space can be guaranteed. The logarithmic spiral, space around the flame, and the position considering different t on the curve are illustrated as follows:

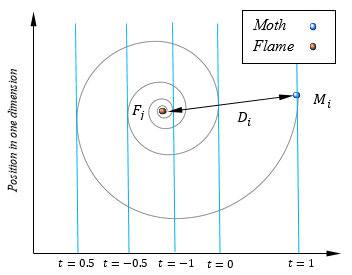This followng figure shows a conceptual model of position updating of a moth around a flame.

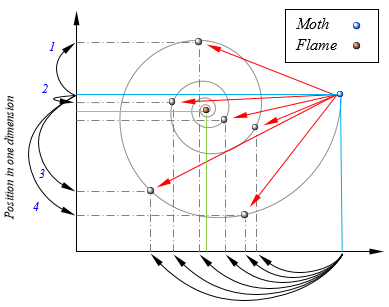Some of the possible positions that can be reached by a moth with respect to a flame using the logarithmic spiral

Note that the vertical axis shows only one dimension (1 variable/parameter of a given problem), but the proposed method can be utilised for changing all the variables of the problem. The possible positions (dashed black lines) that can be chosen as the next position of the moth (blue horizontal line) around the flame (green horizontal line) clearly show that a moth can explore and exploit the search space around the flame in one dimension. Exploration occurs when the next position is outside the space between the moth and flam as can be seen in the arrows labelled by 1, 3, and 4. Exploitation happens when the next position lies inside the space between the moth and flame as can be observed in the arrow labelled by 2. There are some interesting observations for this model as follow:

A moth can converge to any point in the neighbourhood of the flame by changing t

The lower t, the closer distance to the flame.

The frequency of position updating on both sides of the flame is increased as the moth get closer to the flame

The proposed position updating procedure can guarantee the exploitation around the flames. In order to improve the probability of finding better solutions, we consider the best solutions obtained so far as the flames. So, the matrix F in above equations always includes n recent best solutions obtained so far. The moths are required to update their positions with respect to this matrix during optimization. In order to further emphasize exploitation, we assume that t is a random number in [r,1] where r is linearly decreased from -1 to -2 over the course of iteration. Note that we name r as the convergence constant. With this method, moths tend to exploit their corresponding flames more accurately proportional to the number of iterations.

A question that may rise here is that the proposed position updating only requires the moths to move towards a flame, yet it causes the MFO algorithm to be trapped in local optima quickly. In order to prevent this, each moth is obliged to update its position using only one of the flames. It each iteration and after updating the list of flames, the flames are sorted based on their fitness values. The moths then update their positions with respect to their corresponding flames. The first moth always updates its position with respect to the best flame, whereas the last moth updates its position with respect to the worst flame in the list. The following figure shows how each moth is assigned to a flame in the list of flames.

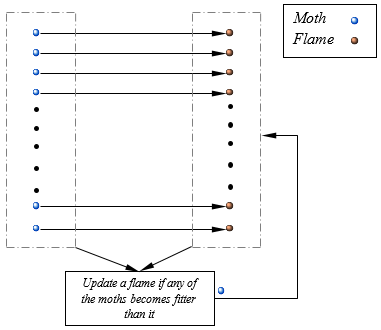It should be noted that this assumption is done for designing the MFO algorithm, while possibly it is not the actual behaviour of moths in nature. However, the transverse orientation is still done by the artificial moths. The reason that why a specific flame is assigned to each moth is to prevent local optimum stagnation. If all of the moths get attracted to a single flame, all of them converge to a point in the search spaces because they can only fly towards a flame and not outwards. Requiring them to move around different flames, however, causes higher exploration of the search space and lower probability of local optima stagnation.

The exploration of the search space around the best locations obtained so far is guaranteed with this method due to the following reasons:

Moths update their positions in hyper spheres around the best solutions obtained so far.

The sequence of flames is changed based on the best solutions in each iteration, and the moths are required to update their positions with respect to the updated flames. Therefore, the position updating of moths may occur around different flames, a mechanism that causes sudden movement of moths in search space and promotes exploration.

Another concern here is that the position updating of moths with respect to n different locations in the search space may degrade the exploitation of the best promising solutions. To resolve this concern, I proposed an adaptive mechanism for the number of flames. The following figure shows that how the number of flames is adaptively decreased over the course of iterations.

Number of flame is adaptively decreased over the course of iterations

I used the following formula to update the nuber of flames over the cource od iterations:

where l is the current number of iteration, N is the maximum number of flames, and T indicates the maximum number of iterations.

The preceding figure shows that there is N number of flames in the initial steps of iterations. However, the moths update their positions only with respect to the best flame in the final steps of iterations. The gradual decrement in number of flames balances exploration and exploitation of the search space.

After all, the general steps of the proposed MFO algorithm in one iteration are presented as follows.

Update flame no using the Equation discussed above      
OM=FitnessFunction(M);

if iteration==1
F=sort(M);
OF=sort(OM);
else
F=sort(Mt-1, Mt);
OF=sort(Mt-1, Mt);
end

for i = 1 : n
for j= 1 : d
Update r and t
Calculate D with respect to the corresponding flame
Update M(i,j) with respect to the corresponding flame
end
end

Of course, we have to create an initial population of moths and regularly update the flames and positions over a desired number of iterations to solve our problems.

I do not want to present the results of the paper here, so you may refer to the paper for more information. I have tested the proposed MFO on several test functions. The results showed the merits of my proposed algorithms in solving optimization problems. I also optimized the shape of several engineering design problems as well as a 6-blade marine propeller in the paper. Here are the 3D/2D models of the problems and propeller.

You can find the details of all problems in the paper. I will explain the propeller design problem quickly. This problem of propeller design has two objectives: cavitation versus efficiency. These two objectives are in conflict and restricted by a large number of constraints as other Computational Fluid Dynamics (CFD) problems. I only maximize the efficiency in this paper.

the main structural parameters are the shapes of airfoils along the blades, which define the final shape of the propeller. The structure of each airfoil is determined by two parameters: maximum thickness and chord length. I considered ten airfoils along the blade in the paper, so there was a total of 20 structural parameters to be optimized by the MFO algorithm. Since the problem of submarine propeller design has many constraints, MFO should be equipped with a constraint handling method. For simplicity, I utilized a death penalty, which assigns very low efficiencyto the artificial moths that violate any of the constraints. Therefore, they are discarded automatically in the next iteration. The final optimial propeller is illustrated as follows:

You see how the performance of MFO paid off in ths real challengin problem. When you see that your algorithm solves such problems, it is really really pleasing. Well done MFO :)

As always, I am gonna share the source codes to be used by anyone who is interested and hope that you find it of some use in your research.

The source codes of MFO are available here.

The Matlab Toolbox of MFO is available here.

You can download the paper here.

If you have no access to Sciencedirect, drop me an e-mail here and I will send you the paper. Please also do not hesitate to contact me for any questions and criticisms. I am always happy to hear your thoughts.

If you have any questions or something to share, please feel free to post it at the end of this page in the comment section.

References

[1] K. J. Gaston, J. Bennie, T. W. Davies, and J. Hopkins, "The ecological impacts of nighttime light pollution: a mechanistic appraisal," Biological reviews, vol. 88, pp. 912-927, 2013.
[2] K. D. Frank, C. Rich, and T. Longcore, "Effects of artificial night lighting on moths," Ecological consequences of artificial night lighting, pp. 305-344, 2006.